贝尔曼方程（第 2 部分）

有两组贝尔曼方程：(1) 贝尔曼预期方程 和 (2) 贝尔曼最优性方程。每组方程包含两个方程，对应于状态值或动作值。

所有贝尔曼方程对有限马尔可夫决策流程 (MDP) 来说都非常有用，在后续课程中还会经常出现。

贝尔曼预期方程

我们已经介绍了 v_\pi 的贝尔曼预期方程

v_\pi(s) = \text{} \mathbb{E}\pi[R{t+1} + \gamma v_\pi(S_{t+1}) | S_t=s]。

之前在这节课中，你发现对于任意随机性策略 \pi，该方程可以表示为

v_\pi(s) = \sum_{s' \in \mathcal{S}^+, r\in\mathcal{R}, a \in \mathcal{A}(s)}\pi(a|s)p(s',r|s,a)(r + \gamma v_\pi(s'))。

该方程表示了任何状态（根据任意策略）相对于后续状态（根据同一策略）的值。

q_\pi 的贝尔曼预期方程是：

q_\pi(s,a) = \text{} \mathbb{E}\pi[R{t+1} + \gamma q_\pi(S_{t+1},A_{t+1}) |S_t=s,A_t=a]

= \sum_{s' \in \mathcal{S}^+, r\in\mathcal{R}}p(s',r|s,a)(r + \gamma\sum_{a' \in \mathcal{A}(s)} \pi(a'|s') q_\pi(s',a'))

其中最后一个形式详细介绍了如何计算任意随机策略 \pi 的预期值。该方程表示任何状态动作对（根据任意策略）相对于后续状态的值（根据同一策略）的值。

贝尔曼最优性方程

和贝尔曼预期方程相似，贝尔曼最优性方程可以证明：状态值（以及动作值函数）满足递归关系，可以将状态值（或状态动作对的值）与所有后续状态（或状态动作对）的值联系起来。

虽然贝尔曼最优性方程关心的是任意策略，但是贝尔曼最优性方程完全侧重于最优策略对应的值满足的关系。

v_* 的贝尔曼最优性方程是：

v_(s) = \max_{a \in \mathcal{A}(s)} \mathbb{E}[R_{t+1} + \gamma v_(S_{t+1}) | S_t=s] = \max_{a \in \mathcal{A}(s)}\sum_{s' \in \mathcal{S}^+, r\in\mathcal{R}}p(s',r|s,a)(r + \gamma v_*(s'))

它表示任何状态根据最优策略相对于后续状态的值（根据最优策略）的值。

q_* 的贝尔曼最优性方程是：

q_(s,a) = \mathbb{E}[R_{t+1} + \gamma \max_{a'\in\mathcal{A}(S_{t+1})}q_(S_{t+1},a') | S_t=s, A_t=a]

= \sum_{s' \in \mathcal{S}^+, r\in\mathcal{R}}p(s',r|s,a)(r + \gamma \max_{a'\in\mathcal{A}(s')}q_*(s',a'))

它表示任何状态动作对根据最优策略相对于后续状态动作对（根据最优策略）的值的值。

实用公式

为了推导出所有四个贝尔曼方程，有必要先推导出紧密相关的公式。

q_\pi(s,a) = \sum_{s'\in\mathcal{S}^+, r\in\mathcal{R}}p(s',r|s,a)(r+\gamma v_\pi(s')) (方程 1)

该方程表示相对于状态值函数和 MDP 一步动态特性的策略动作值函数。

我们将提供两个论证来证明该方程，一个是对话论证，另一个是代数论证。

求导 1

我们将先从会话参数开始。当智能体位于状态 s 并采取动作 a 时，可以产生任何数量的潜在下个状态 s'' 和奖励 r。

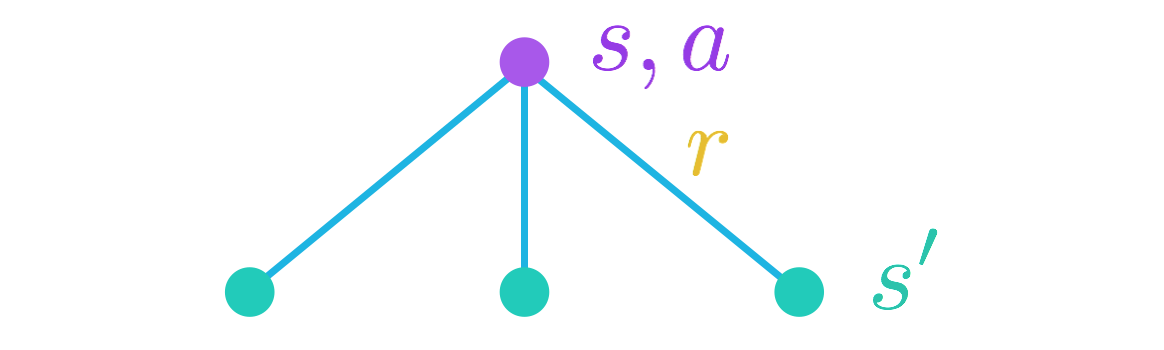
如果下个状态 s' 和奖励 r 可以确切地预测，那么回报可以计算为 r + \gamma v_\pi(s')。

知道这一点后，为了获得动作值 q_\pi(s,a)，我们只需计算和 r + \gamma v_\pi(s') 的预期值。可以通过以下方程获得

q_\pi(s,a) = \sum_{s'\in\mathcal{S}^+, r\in\mathcal{R}}p(s',r|s,a)(r + \gamma v_\pi(s'))，

其中每个 s',r 对的概率由 MDP 的一步动态特性 p(s',r|s,a) 确定。

求导 2

请算出以下方程 1 的替代导数。

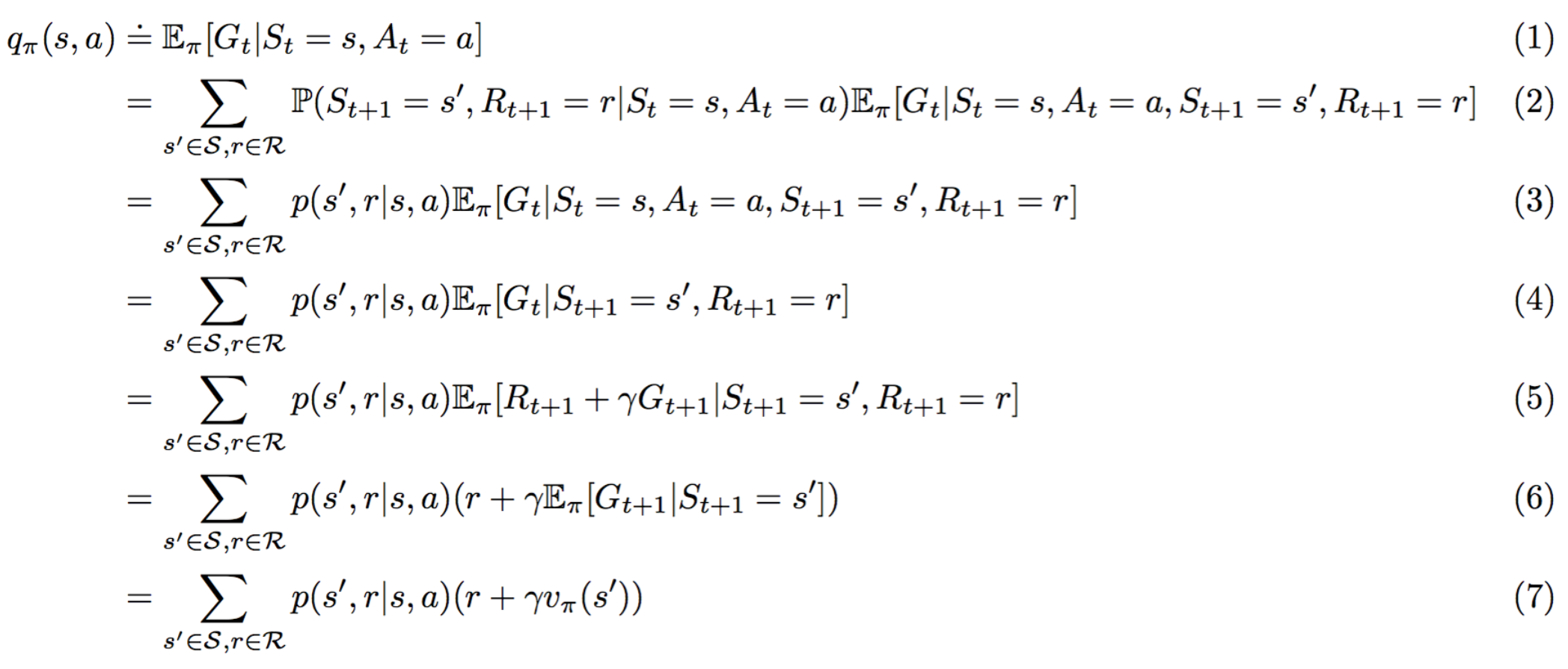
理由如下：

(1) 满足 q_\pi(s,a) := \mathbb{E}_\pi[G_t|S_t=s, A_t=a] 的定义。
(2) 遵守全期望公式。
(3) 根据定义 p(s',r|s,a) := \mathbb{P}(S_{t+1}=s',R_{t+1}=r|S_t=s,A_t=a) 是正确的
(4) 满足，因为 \mathbb{E}\pi[G_t|S_t=s,A_t=a,S{t+1}=s',R_{t+1}=r]=\mathbb{E}\pi[G_t|S{t+1}=s',R_{t+1}=r]。
(5) 遵守，因为 G_t = R_{t+1}+G_{t+1}。
(6) 根据线性期望是正确的。
(7) 根据定义 v_\pi(s') := \mathbb{E}\pi[G_t|S_t=s']=\mathbb{E}\pi[G_{t+1}|S_{t+1}=s'] 是正确的。

得出贝尔曼预期方程

为了得出贝尔曼预期方程，我们需要使用另一个公式。

v_\pi(s) = \sum_{a\in\mathcal{A}(s)}\pi(a|s) q_\pi(s,a)（方程 2）

该方程使我们能够根据（潜在随机性）策略对应的动作值函数获得状态值函数。

v_\pi 的贝尔曼预期方程可以通过先从方程 2 开始并用方程 1 替换 q_\pi(s,a) 的值获得。

同样，q_\pi 的贝尔曼预期方程可以通过先从方程 1 开始并用方程 2 替换 v_\pi(s) 的值获得。

获得贝尔曼最优性方程

为了推出贝尔曼最优性方程，我们需要另外两个方程。

q_(s,a) = \sum_{s'\in\mathcal{S}^+, r\in\mathcal{R}}p(s',r|s,a)(r+\gamma v_(s')) (方程 3)

方程 3 表示相对于最优状态值函数和 MDP 一步动态特性的最优动作值函数。

v_(s) = \max_{a\in\mathcal{A}(s)} q_(s,a) (方程 4)

方程 4 表示相对于最优动作值函数的最优状态值函数。

v_ 的贝尔曼最优性方程可以通过先从方程 4 开始并用方程 3 替换 q_(s,a) 的值获得。

q_ 的贝尔曼最优性方程可以通过先从方程 3 开始并用方程 4 替换 v_(s) 的值获得。

13. 贝尔曼方程（第 2 部分）